Hacía tiempo que no me ponía a mi mismo un reto de programación y el otro día viendo en la tele el programa cifras y letras me animé a hacer una aplicación que resolviese la sección de cifras. Primero me leí las normas y luego empecé a pensar cómo resolver este tipo de problema. Buscando por Internet encontré estos artículos: (uno, dos y tres) donde de 30.965.760 combinaciones posibles entre los 6 números y sus cuatro operaciones se reduce a 488.642 combinaciones. Además me encontré con dos páginas que resuelven el problema on-line: esta y esta (ambas usando la técnica de backtracking).
Como mi objetivo era hacerlo mediante fuerza bruta, la técnica de backtracking me pareció lo mejor para abordar el problema. Se crea un árbol donde cada nodo contendrá los números con los que se operan, la operación que ha generado ese nodo y el resultado de la misma (excepto el primer nodo que sólo contiene el conjunto de números original).
Vamos combinando uno por uno todos los números con todas las operaciones para encontrar el resultado que buscamos. El orden de las operaciones es suma, resta, multiplicación y división. Como esto puede generar una ingente cantidad de cálculos, podemos podar (acotar) el árbol para reducir estos y el tiempo empleado. Esto se consigue eliminando aquellos casos que no deben darse: En la resta que el resultado sea 0, en la división que el divisor sea 1 o que el resto sea distinto de 0 y que en la multiplicación uno de los factores sea 1. Para evitar números negativos en la resta o que el divsor sea mayor que el dividendo ponemos primero el mayor y después el menor en la operación.
A medida que vamos avanzando en la profundidad del árbol, el conjunto de números con los que operar se irá reduciendo ya que cada pareja de números se convertirá en uno por la operación matemática que se les aplique, siendo esto así recursivamente hasta que sólo haya un número, momento en el cual si el resultado no coincide con el esperado, se retrocede un nodo y se continúa con las siguientes combinaciones.
Para entenderlo mejor un gráfico donde dado un conjunto de tres números (1, 2 y 3) debemos operar con ellos hasta que obtengamos 7 como resultado:
![]()
En el ejemplo después de buscar varias combinaciones entre sumas y restas (puntos suspensivos en el gráfico) hemos llegado a las combinaciones de multiplicaciones. Existen tres combinaciones de multiplicaciones: Op: 1 * 2 (que no he puesto en el gráfico por simplificarlo), Op: 1 * 3 y Op: 2 * 3.
- En el nodo de la multiplicación de 1 * 3 el resultado (Res:) es 3 y no 7 como andamos buscando por lo que hay que seguir calculando. El conjunto de números de este nodo se ha reducido de Nu: 1, 2, 3 a Nu: 2, 3.
- A continuación hay que crear otro nodo con la suma de los únicos números que quedan: 2 + 3, pero el resultado es 5 con lo que volvemos al nodo anterior.
- Vamos a hacer la resta: 3-2, pero sigue sin servirnos el resultado, por tanto volvemos al nodo anterior.
- Hacemos la multiplicación: 2 * 3, pero seguimos igual, por lo que nos vamos al nodo anterior.
- La división se descarta porque 3 / 2 no dá como resto 0, con lo que no se crea ese nodo y se vuelve al anterior (que en este ejemplo es el principal).
- Continuamos con la creación del nodo de la multiplicación de 2 * 3 donde el resultado (Res:) es 6 y no 7 como andamos buscando por lo que hay que seguir calculando. El conjunto de números de este nodo se ha reducido de Nu: 1, 2, 3 a Nu: 1, 6.
- Hay que crear otro nodo con la suma de los únicos números que quedan: 1 + 6, y como el resultado es 7, que es el que buscábamos, ya no hacemos ninguna operación más y vamos retrocediendo por todo el árbol (que os recuerdo que se ha construido mediante una función recursiva) hasta salir de la función que lo ha generado.
El nivel de profundidad de los árboles depende de la cantidad de números inicial. Si son un conjunto de 3 números la profundidad será de 3 niveles, si es de 6 pues … ya sabeis la respuesta 🙂
Como se trata de una estructura de árbol, cada nodo debe tener un puntero al siguiente nodo para trazar un camino desde el nodo inicial hasta el nodo que contiene el resultado que buscamos (en el cual el puntero estará vacío). Dado que hemos aplicado la técnica de backtracking los nodos que previamente hayamos calculado y no pertenezcan a ese camino desaparecerán porque no nos sirven. Finalmente mediante un bucle recorreremos todos los nodos del camino mostrando por pantalla la operación que lo ha creado hasta el nodo final. Así en el ejemplo quedaría:
|
1 2 |
3 * 2 = 6 6 + 1 = 7 |
Sin embargo en el juego de cifras y letras si no se encuentra el número exacto se puntúa el número que más se acerque a este. La problemática aquí es que con el bactracking, si no se encuentra el número exacto, el camino que se habrá generado cuando retorne la función es el de la última operación, que con toda probabilidad no será el camino hacia el número que más se aproxime al original.
En este caso tenemos dos posibles formas de solucionarlo:
- A medida que vamos generando los nodos debemos comparar el resultado con el número que buscamos, si se acerca más que el anterior valor que hayamos comparado guardamos este resultado como el número que más se aproxima al buscado. Después cuando haya salido de la función y no se haya encontrado el exacto, se vuelve a llamar a esta misma pero buscando en esta ocasión el resultado aproximado (ya que tenemos la certeza de que se puede calcular) obteniendo así el camino hasta llegar al que más se acerca.
- El problema de la solución anterior es que tenemos que llamar dos veces a la función que genera el árbol: una para buscar el exacto y otra para buscar el aproximado. Lo ideal es ir guardando un camino alternativo hacia el número aproximado, para que, en caso de no hallar el exacto, recorrer el camino alternativo mediante un bucle para mostrar las operaciones que obtengan el número aproximado. Todo desde la misma llamada a la función. Esto provoca que también se necesite un puntero al nodo anterior.
Aquí dejo el código fuente en C# que pone en práctica todo lo comentado. Se trata de una aplicación de consola donde como parámetros se le pasa todo el conjunto de números separados por espacio y como último número el resultado que se desea averiguar.
Program.cs:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
using System; using System.Collections.Generic; using System.Collections; using System.Text; namespace Cifras { class Program { static int Main(string[] args) { // Ncesitamos como mínimo dos números para operar y un resultado if (args.Length < 3) { Console.Write("La sintaxis es " + System.AppDomain.CurrentDomain.FriendlyName + " <número 1>...<número n> <número buscado>"); return 1; } Console.Write("Set de números: "); ArrayList posibilidades = new ArrayList(); int indice = 0; // Creamos el conjunto de números a partir de la línea de comandos. for (; indice < args.Length - 1; indice++) { Console.Write(args[indice] + " "); posibilidades.Add(Int32.Parse(args[indice])); } int descubre = Int16.Parse(args[indice]); Console.WriteLine("\nNúmero buscado: " + descubre + "\n"); // Creamos el primer nodo del árbol. Nodo encuentra = new Nodo(posibilidades, descubre); // Creamos un contador DateTime hora = DateTime.Now; TimeSpan tiempo; // Si se ha encontrado el exacto if (encuentra.busca() == true) { tiempo = DateTime.Now - hora; Console.WriteLine("Se encontró el exacto.\n"); } // En caso de no encontrarse el exacto else { tiempo = DateTime.Now - hora; Console.WriteLine("No se ha encontrado el exacto.\n"); // Sustituimos el camino original por el camino del aproximado encuentra = Nodo.Cercano; } Console.WriteLine("Número de nodos calculados: " + Nodo.NumeroNodos); Console.WriteLine("Tiempo en calcularlo: " + tiempo.TotalMilliseconds + " ms.\n"); Console.WriteLine("Operaciones:"); // Recorremos todos los nodos del camino para mostrar las operaciones que se han ido ejecutando. while (encuentra.Hijo != null) { encuentra = encuentra.Hijo; Console.WriteLine(encuentra.Valor1 + encuentra.Signo + encuentra.Valor2 + "=" + encuentra.Resultado); } return 0; } } } |
Nodo.cs:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 |
using System; using System.Collections.Generic; using System.Collections; using System.Text; namespace Cifras { class Nodo { private enum OPERACIONES { SUMA, RESTA, MULTIPLICACION, DIVISION }; private static int buscado; // El número exacto que debemos encontrar. private ArrayList numeros; // El conjunto de números con los que pueden operar los hijos del nodo. private Nodo padre; // El nodo padre del nodo actual. private Nodo hijo; // El nodo hijo del nodo actual. public Nodo Hijo { get { return hijo; } } private int valor1; // El primer operando. public int Valor1 { get { return valor1; } } private int valor2; // El segundo operando. public int Valor2 { get { return valor2; } } private string signo; // El signo de la operación. public string Signo { get { return signo; } } private int resultado; // El resultado de la operación. public int Resultado { get { return resultado; } } private static Nodo cercano; // Camino donde se llega al número más aproximado al buscado. public static Nodo Cercano { get { return Nodo.cercano; } } private static int aproximado; // Variable que va guardando qué número es el más aproximado. private static int numeroNodos; // Número total de nodos creados. public static int NumeroNodos { get { return Nodo.numeroNodos; } } // Contructor para crear el primer nodo del arbol public Nodo(ArrayList numeros, int buscado) { this.numeros = numeros; Nodo.buscado = buscado; padre = null; hijo = null; Nodo.cercano = null; Nodo.aproximado = 0; Nodo.numeroNodos = 0; } // Constructor para crear los restantes nodos del arbol. private Nodo(ArrayList numeros, int valor1, int valor2, int resultado, string signo, Nodo padre) { this.numeros = numeros; this.valor1 = valor1; this.valor2 = valor2; this.resultado = resultado; this.signo = signo; this.padre = padre; this.hijo = null; // Para saber cuantos nodos se han creado. Nodo.numeroNodos++; // Vamos guardando el número cercano más próximo al buscado. if (Math.Abs(buscado - resultado) < Math.Abs(buscado - aproximado)) { // Creamos un camino alternativo duplicando los nodos. // Esto es necesario porque en backtracking los nodos que no sirven se eliminan y necesitamos // tener un camino hacia el resultado aproximado que perdure en toda la ejecución de la función. Nodo historico = this; Nodo copia = (Nodo)this.MemberwiseClone(); while (historico.padre != null) { copia.padre = (Nodo)historico.padre.MemberwiseClone(); copia.padre.hijo = copia; historico = historico.padre; copia = copia.padre; } cercano = copia; aproximado = resultado; } } // La función principal que busca el resultado combinando el conjunto de números del nodo con las // operaciones de suma, resta, multiplicación y división. public bool busca() { // Si el nodo actual contiene el número buscado ya no hacemos más búsquedas if (resultado == buscado) { return true; } // Vamos recorriendo cada elemento del conjunto de números operándolo con los demás. for (int indice1 = 0; indice1 < numeros.Count; indice1++) { for (int indice2 = indice1 + 1; indice2 < numeros.Count; indice2++) { if (calculos(indice1, indice2, OPERACIONES.SUMA) == true) { return true; } if (calculos(indice1, indice2, OPERACIONES.RESTA) == true) { return true; } if (calculos(indice1, indice2, OPERACIONES.MULTIPLICACION) == true) { return true; } if (calculos(indice1, indice2, OPERACIONES.DIVISION) == true) { return true; } } } // Si llegamos aquí es que todos los cálculos en esta rama del arbol han sido infructuosos. return false; } // Esta función crea un nuevo nodo después de operar los números. Le asigna un nuevo conjunto de números, // el resultado de la operación, y los números involucrados. private bool calculos(int indice1, int indice2, OPERACIONES operacion) { int resultado = 0; string signo = ""; int valor1 = (int)numeros[indice1]; int valor2 = (int)numeros[indice2]; // Hacemos que en la resta, división y multiplicación el primer operando sea mayor que el segundo if ((operacion == OPERACIONES.RESTA) || (operacion == OPERACIONES.DIVISION) || (operacion == OPERACIONES.MULTIPLICACION)) { if (valor1 < valor2) { int valor3 = valor1; valor1 = valor2; valor2 = valor3; } } // Calculamos la operación con los números, haciendo la poda del arbol si es necesario. switch (operacion) { case OPERACIONES.SUMA: resultado = valor1 + valor2; signo = "+"; break; case OPERACIONES.RESTA: if ((valor1 - valor2) == 0) // Un número que da cero no sirve para seguir { return false; } resultado = valor1 - valor2; signo = "-"; break; case OPERACIONES.MULTIPLICACION: if (valor2 == 1) // Una multiplicación que por 1 da el mismo resultado no sirve { return false; } resultado = valor1 * valor2; signo = "*"; break; case OPERACIONES.DIVISION: if ((valor2 == 1) || ((valor1 % valor2) != 0)) // Un división que por 1 da el mismo resultado o que tiene decimales no sirve { return false; } resultado = valor1 / valor2; signo = "/"; break; } // Generamos el nuevo conjunto de números sobre los que operar. ArrayList posibilidades = new ArrayList(); posibilidades.Add(resultado); for (int indice = 0; indice < numeros.Count; indice++) { // No permitimos que se incluyan los números que ya se han operado. if ((indice != indice1) && (indice != indice2)) { posibilidades.Add(numeros[indice]); } } // Creamos el nuevo nodo. Nodo opcion = new Nodo(posibilidades, valor1, valor2, resultado, signo, this); // Hacemos la búsqueda recursiva. Si lo encontramos vamos generando el camino hacia el nodo con el // número exacto. if (opcion.busca() == true) { hijo = opcion; return true; } else { return false; } } } } |
También podéis descargaros el ejecutable del programa para poder hacer las pruebas.
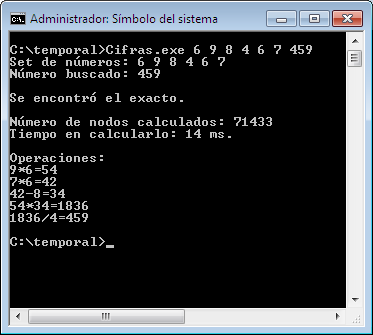
Así por ejemplo este reto:
Se resuelve como:
Es una buena primera aproximación, pero en realidad te dejas a un lado otro set de operadores. Por ejemplo:
Sumo 3 + 7 por un lado
Sumo 4 + 2 por otro
Multiplico los resultantes (10 * 6)
¿Se podría llegar a 60 utilizando cada uno de los 4 números por su cuenta y con las operaciones previstas?… Problema para el programa 😉
En realidad, deberíamos considerar cualquier par de números producto cartesiano con las operaciones como otros posibles operadores, e incluso cada trio o n-tupla.
Así te dará mejores soluciones (o más cercana), pero necesita de mucha más fuerza.
En principio eso es lo que hace, he probado lo que me dices y esto es lo que sale:
C:\temporal>Cifras.exe 3 7 4 2 60
Set de números: 3 7 4 2
Número buscado: 60
Se encontró el exacto.
Número de nodos calculados: 39
Tiempo en calcularlo: 11,0011 ms.
Operaciones:
3+7=10
4+2=6
10*6=60
Desde luego no siempre la solución es la que un humano pensaría hacer intentando sacar el menor número de operaciones, ya que computacionalmente es más rápido buscar la primera solución que la más optima.
Ah, cojonudo entonces, no me había dado la impresión por el post de que también fuera capaz de agrupar, y por tiempo no pude leerme el código a fondo 🙁
Pues nada, ahora a ir al programa y a hacerse ricos! 😉
Es lo que tiene la fuerza bruta, al final sale la combinación 🙂
Y no te preocupes, que no creo que nadie se lea el código fuente XD